More detailed data analysis including Kriging using R and fields

For all of these examples you should load the fields package and also the datasets. (You only need to do this once when starting R.) Fields is available as a contributed package in the Comprehensive R Archive Network CRAN

Load the fields library and the binary version of MJ data set

library(fields)
attach("RData.riflesight.bin")

Some preliminaries: converting lon/lat grid to an approxmiate Euclidean grid in meters

Note that the perspective and image plots actually use the lon lat coordinates. But the Euclidean transformation is used for surface fitting and estimating derivatives.

# find spacing in meters of the lon and lat grid.
# and scale of longitude coordinates to give equal distance
# Because this region is so small we will ignore the curvature of
# coordinates on sphere.
 
dlat<- RifleDEM$y[2]- RifleDEM$y[1]

dx<- rdist.earth( cbind( RifleDEM$x[1:2],  RifleDEM$y[c(1,1)] ),
  miles=FALSE)[2,1] *1000
dy<- rdist.earth( cbind( RifleDEM$x[c(1,1)],  RifleDEM$y[1:2] ) , 
   miles=FALSE)[2,1] *1000

dlon<- RifleDEM$x[2]- RifleDEM$x[1]
dlat<- RifleDEM$y[2]- RifleDEM$y[1]

# Create all the grid locations explicitly
# converting  to a approximate cartesian grid in meters

make.surface.grid( list( x=(RifleDEM$x- RifleDEM$x[1])*dx/dlon, 
                         y= (RifleDEM$y- RifleDEM$y[1])*dy/dlat) )-> Rgrid

# Rtrial is the ski run in the meter Euclidean coordinates.
Rtrail<- cbind( 
 (rifle.trail[,1] - RifleDEM$x[1])*dx/dlon,
 (rifle.trail[,2] - RifleDEM$y[1])*dy/dlat )

# to find slopes need to parameterthe 1-d curve of the ski run 
# by arc length
 N<- nrow( rifle.trail)
 rD<- sqrt(diff( Rtrail[,1])**2 + diff( Rtrail[,2])**2)
 trail.D<- c(0,cumsum( rD))

Calculating a variogram of the elevations to look at spatial dependence

See VG.html for some detailed source code for fitting the variograms to short ranges.

#First remove spatial linear drift by least squares fit before finding 
# the variogram.
zR<- lsfit( Rgrid, c( RifleDEM$z))$residuals
zR<- matrix( zR, ncol= ncol( RifleDEM$z), nrow= nrow( RifleDEM$z))

# see help(vgram.matrix) for details on this function
# R is set to look at all pairs within a distance of about 6.5 grid spacings

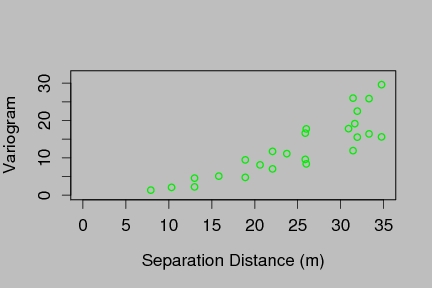
vgram.matrix( zR, R= 65, dx=dx, dy=dy) -> look

# A nice plot converting distance in scaled lon/lat to meters.

fields.style()
plot( look$d.full, look$vgram.full, xlab="Separation Distance (m)",
   ylab="Variogram",  xlim=c(0, 35),ylim=c(0,32), col=2)

What you have been waiting for: Interpolating the DEM elevations to the locations of the actual run.

# Kriging with compactly supported Wendland covariance function
# The range (theta) controls support. 

theta<- 30
lambda<-0

mKrig( Rgrid, c( RifleDEM$z), cov.function="wendland.cov", k=2,
             theta=theta,
             lambda=lambda,mean.neighbor=50 )-> rifle.fit

rifle.trail.elev<- predict(rifle.fit, Rtrail)

Calculating the slope along the ski run two ways

# computing slope based on 1-d space curve 
# and interpolating cubic spline
  trail.slope<- splint( trail.D,rifle.trail.elev, trail.D, derivative=1)
  trail.degrees<- - atan( trail.slope)*(360/(2*pi))

# The correct way to find by slope taking partials of elevation surface
# 
  rifle.trail.der<- predict(rifle.fit, Rtrail,derivative=1)

# First find unit tangent vector along run
#
 xp<- splint( trail.D,rifle.trail[,1], trail.D, derivative=1)
 yp<- splint( trail.D,rifle.trail[,2], trail.D, derivative=1)
 R<- sqrt( xp**2 + yp**2)
 xp<- xp/R
 yp<- yp/R

# find directional derivative based on tangent vector

 trail.slope2<-  xp*rifle.trail.der[,1] + yp*rifle.trail.der[,2]
 trail.degrees2<- - atan( trail.slope2)*(360/(2*pi))

It can be checked that the two estimates of slope are very similar.

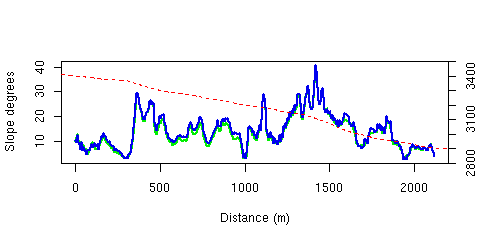
  matplot( trail.D, cbind(trail.degrees,trail.degrees2),
                      type="l", xlab="Distance (m)", 
              ylab="Slope degrees",lwd=2, col=c(2,3),lty=1 )

# Just for fun ... add in elevation drop 
  par( usr=c(0,2000,2800,3500) )
  lines( trail.D, rifle.trail.elev,type="l", xlab="Distance (m)",
                ylab="Elevation (m)",col=4, lwd=1.5, lty=2)
  axis( 4)

DISCLAIMER:

The data sets, software and related content in and linked to these pages are intended for scientific and mathematical research. The authors do not guarantee the correctness of the data, software or companion text. Please see the UCAR Terms of Use listed below.