1 dimensional example (cont.)
Diagonalizing
U(m,n) determines the eigenvalues and
eigenvectors of U(m,n). The sum of the eigenvalues
is
the trace of the U and is an
invariant corresponding
to
the total variance. The diagonalization
breaks the variance
into
independent pieces and the eigenvalue is the variance in
each
independent piece. The eigenvectors are the spatial
structures
corresponding to each independent variance
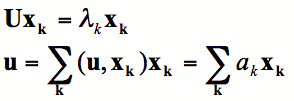
Eigenvectors are orthogonal and can be used
as
a basis for u