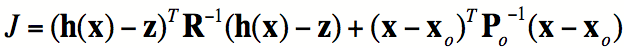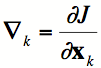Estimation
as minimization
§Solve for
x with an approximate, iterative method rather than an exact matrix inversion
§Start with
guess x0, compute gradient
efficiently
with an adjoint model, search for minimum along -„, compute
new „ and repeat
§Good for non-linear
problems; use conjugate gradient or BFGS
approaches
§Low-rank
covariance matrix built up as iterations progress
§As with
Kalman filter, transport errors can be handled as dynamic noise