-
- Sponsors
- Workshop
- Boulder
| |
 |
The Institute for Mathematics Applied to Geosciences
Theme for 2009: The Interaction of Simulation and Numerical Models
|
Free Boundary Problems
24 - 25 August 2009, Boulder, Colorado
ABSTRACTS
NCAR Scientists
Free-Boundary Problems Rising from the Magnetohydrodynamics of the Solar Atmosphere
B C Low
With its astronomical scales, the ionized, magnetized solar atmosphere is a natural laboratory for ideal magnetohydrodynamic (MHD) processes and phenomena. Magnetic flux surfaces evolve as fluid surfaces. This property gives rise to problems of free boundaries separating fluids kept apart in distinct thermodynamic states. The three fundamental modes of ideal MHD waves give rise to the three corresponding types of shock waves as another class of free boundaries, those that propagate across fluids. These phenomena of sharp boundaries have been directly observed with impressive spatial and temporal resolutions in solar physics. This talk is directed at some basic phenomenology to lead to the first class of free boundary problems, describing, in particular, equilibrium magnetic fields in different states of twist separated by flux surfaces as tangential discontinuities in the field, and, time-dependent spontaneous formation of such magnetic tangential discontinuities as a topological problem.
Lock-Exchange Flow
Rich Rotunno
Based on work with J. Klemp, G. H. Bryan and D. Muraki
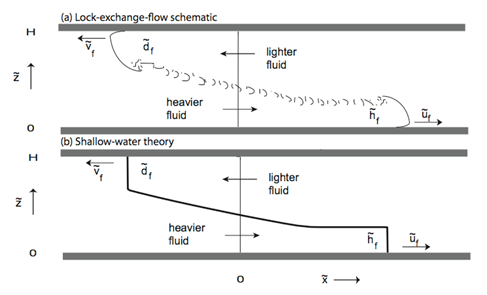
Lock-exchange flow results from the adjustment under gravity of two fluids of different densities that are initially separated by a vertical partition in a horizontal channel (Fig. 1a). In addition to gravity and pressure-gradient forces, a model of lock-exchange flow must reckon with stress at the horizontal channel walls, stress and diffusion between the two fluids and, in cases involving a liquid-gas interface, surface-tension effects. Given the mathematical complexity attaching to these processes, the more tractable two-layer shallow-water equations, in which the aforementioned processes are either neglected or simply represented, have been applied to lock-exchange flow to provide a basic guide to flow behavior. I will present analytical solutions to the two-layer shallow-water equations of lock-exchange flow (Fig. 1b) across the range of the ratio of light- to the heavy-fluid densities. As the latter solutions assume a ‘front’ condition (where the shallow-water approximation is not accurate), I will show some solutions to the Navier-Stokes equations for parameter settings relevant to the shallow-water theory. Agreement is generally good, but conceptual problems remain, and I will seek advice and opinions on them from the participants.
| |
 |
|
Coupling the Dynamics of Boundary Layers and Evolutionary Dunes
Piotr Smolarkiewicz
A novel theoretical formulation and corresponding numerical solutions are presented for fluid flow and sediment transport past evolutionary sand dunes. From the theoretical view point, dunes development and accompanying sand transport is a fundamental dynamical mechanism with challenging detail. In particular, predicting sediment transport and bed evolution in severe wind conditions depends on accurate prediction of a flow past complex boundary evolving with the flow itself.
Time-dependent curvilinear coordinates are employed to fully couple flow aloft with the developing landform. The differential conservation law that defines shape of the lower boundary (viz. landform) depends on details of local surface stress, thereby favoring the large eddy simulation (LES) of the atmospheric boundary layer.
Impacts of Surface Waves on Marine Boundary Layers: Explorations Via Turbulence Simulations
Peter Sullivan
Surface gravity water waves couple turbulent winds and currents in the marine boundary layers over scales from millimeters to hundreds of meters. Waves move randomly, propagate rapidly, support wind stress, break intermittently, force winds in the atmosphere, and induce Langmuir circulations in the ocean. Although these fluid-mechanical processes are basic building blocks in wavy air-water flows they are typically poorly parameterized in large-scale weather and climate models. In this presentation we utilize turbulence resolving simulations, primarily large-eddy simulations, to examine the impacts of waves on winds and currents. Our simulations illustrate how fast moving waves can drive wave-driven winds in the atmosphere and generate Langmuir circulations in the ocean mixed layer.
Visiting Computational Mathematicians
Two New Numerical Methods for Free Boundary Problems
Bengt Fornberg
University of Colorado at Boulder
Free boundaries are ubiquitous in fluid mechanics, plasma physics, etc. They may arise as steady states for moving boundary problems, or they may represent time-unstable equilibria. In either case, they can often be formulated mathematically in terms of elliptic PDEs, with certain compatibility conditions imposed along the (unknown) free boundary. Numerical solution methods should handle both of these situations efficiently and accurately, and also be easy to implement. We will focus here on two new methods that are based on regular finite differences and on radial basis functions, respectively. In both cases, minimax-type optimization (as available for example through Matlab's fminimax routine) gives fast and reliable convergence.
A Marker Level Set Method for Tracking Interfaces in Multiphase Flow
Mark Sussman
Florida State University
We compare the marker level set method (MLS) to the coupled level set and volume-of-fluid method (CLSVOF) for test problems such as Zalesak's problem and the rise of a gas bubble in liquid. Then we apply the MLS method to a two-phase flow problem in which temperature effects are present. For example, we shall simulate the problem of a differentially heated rotating annulus. Given that everything else is equal, the MLS method would be superior to the CLSVOF method in terms of ease of implementation since one does not have to develop complicated geometric operations when implementing the MLS method on curvilinear grids or unstructured grids. Also, if the underlying grid is dynamic, one must introduce logic to conserve mass with the CLSVOF method during regridding.
Educational Activity
Introduction to the level set method for representing and tracking moving boundaries
A sample matlab file will be available in which one can modify the finite difference method used for the level set equation and one can modify the underlying velocity field or initial level set function.
DNS of Multiphase Flows Using a Front-Tracking Method
Gretar Tryggvason
Worcester Polytechnic Institute
Direct numerical simulations have recently emerged as a viable tool to understand finite Reynolds number multiphase flows. The approach parallels DNS of turbulence, but the unsteady motion of a deforming phase boundary adds considerable complexity. After a brief overview of the “one-fluid” formulation of the Navier-Stokes equations for incompressible flows and their numerical implementation, we describe one approach, front-tracking, in some detail. The method has been used to study a large number of multiphase flows and we give a few examples of recent work. Results for drag reduction due to bubbles injected into a turbulent boundary layer, and for buoyancy driven bubbly flows in vertical channels have, for example, yielded new and unexpected insight into the dynamics of such flows and the subtle importance of accurately accounting for bubble deformability. The development of numerical methods for more complex multiphase flows, where it is necessary to include thermal and/or electric fields and phase changes, is also discussed.
Educational Activity
We examine a simple implementation of front-tracking using MATLAB.
Sharp Interface Methods for Moving Boundary Problems
H.S. Udaykumar
The University of Iowa
When moving boundary problems are solved on Cartesian meshes the treatment of the immersed interfaces that arise can be an important issue. Various types of boundary conditions apply (on the field in each subdomain separated by the interface) on these immersed interfaces, viz. Dirichlet type, flux type or jump conditions. Our approach has been to treat these immersed interfaces as sharp entities and to apply the applicable boundary conditions explicitly at the interfaces. A wide range of applications have been tackled in this framework, including phase changes, multiphase flows, fluid-structure interactions, compressible multimaterial flows etc. Interfaces are tracked using standard levelset approach. We will show recent work relating to problems in biofluid dynamics and high-speed multimaterial interactions. Current issues include developing techniques for multiscale modeling and devising ways to go from biomedical imaging to computation in a painless way. Both of these aspects will be highlighted.
|

