

1. Introduction
3. Spatial Process Models: Krig6. Other Fields Functions
Fields is a collection of programs based in S for curve
and function fitting with an emphasis on spatial data. The major methods
implemented as S functions include:
Finally, we note that this manual gives an introduction to many functions but few complete treatments. Please refer to the help files with their examples for more information. The reader is also referred to the Fields demo for some in-depth examples.
The assumed model for Tps is additive. Namely,
Y = f(X) + e,
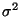 /W_i.
/W_i.
(1/n)*(RSS) + 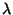 *J_m(f)
*J_m(f)
where RSS is a weighted residual sums of squares: sum
( f(x_i)- y_i)**2 w_i , J_m is a roughness penalty based
on m th order derivatives and 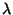 > 0.
> 0.
A thin plate smoothing spline is a generalization of
the cubic smoothing spline, and depends on two parameters: m, the order of the derivative penalty,
and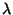 , a parameter controlling the amount of
smoothing. For the case of one dimension and m = 2, the estimate reduces to the usual cubic
spline.
, a parameter controlling the amount of
smoothing. For the case of one dimension and m = 2, the estimate reduces to the usual cubic
spline.
The smoothing parameter,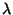 , varies from zero to infinity. When
, varies from zero to infinity. When 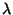 = 0 the spline estimate interpolates the data and
has a residual sums of squares of zero. At the other
extreme,
= 0 the spline estimate interpolates the data and
has a residual sums of squares of zero. At the other
extreme, 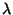 of infinity results in an
estimate that is a polynomial of degree m - 1 with the coefficients estimated by least
squares. In place of
of infinity results in an
estimate that is a polynomial of degree m - 1 with the coefficients estimated by least
squares. In place of 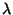 a more useful
scale is in terms of the effective number of parameters (degrees of
freedom) associated with the estimate. We denote this
by EDF(lambda) for effective degree of freedom.
a more useful
scale is in terms of the effective number of parameters (degrees of
freedom) associated with the estimate. We denote this
by EDF(lambda) for effective degree of freedom.
The smoothing parameter can be chosen
from the data by Generalized Cross-Validation (GCV). That is,
the estimate of the smoothing parameter can be found by minimizing the
GCV function
V(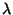 ) = N / D
) = N / D
where N = (1/n) RSS(lambda) and D = (1 - EDF(![]() ) /n)^2. It is also possible to
include a cost parameter that can give more (or less) weight to the
effective number of parameters beyond the base polynomial
model.
) /n)^2. It is also possible to
include a cost parameter that can give more (or less) weight to the
effective number of parameters beyond the base polynomial
model.
A frequentist estimate for the
residual variance, 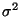 , is found using the
estimate for
, is found using the
estimate for 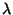 by
by
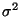 =RSS/ (n-
EDF(lambda))
=RSS/ (n-
EDF(lambda))
ozone is a small Fields data set included for explanatory purposes. It is a list object that has two different versions of grid coordinates: x and lon.lat. Here we use the Cartesian coordinates in x. One can fit a thin plate spline to the y values by
ozone.tps <- Tps( ozone$x, ozone$y)
Generic S-Plus functions such as summary, predict, print, and plot apply to ozone.tps object. For example,
summary(ozone.tps) Call: Tps(x = ozone$x, Y = ozone$y, cov.function = "Thin plate spline radial basis functions (rad.cov)")
1. Number of Observations: 2. Number of unique points: 3. Degree of polynomial null space (base model): 4. Number of parameters in the null space 5. Effective degrees of freedom: 6. Residual degrees of freedom: 7. MLE sigma 8. GCV est. sigma 9. MLE rho 10. Scale used for covariance (rho) 11. Scale used for nugget (sigma^2) 12. lambda (sigma2/rho) 13. Cost in GCV 14. GCV Minimum |
20 20 1 3 4.5 15.5 4.098 4.072 205.8 205.8 16.79 0.0816 1 21.41 |
Residuals: min 1st Q median 3rd Q max -6.801 -1.434 -0.5055 1.439 7.791 REMARKS Covariance function: rad.cov
The top two graphs are typical
regression diagnostic plots. The left lower plot is the GCV function
plotted against effective number of parameters in the spline. Note
minimum at approximately 4.5 agreeing with the summary values. Right
lower plot is a histogram of residuals.
Finally, here is
the simplest example of using the predict function. The default is to
predict at the observed data locations.
ozone.tps.pred <- predict(
ozone.tps) ozone.tps.pred predict( ozone.tps,
other.locations) surface( ozone.tps) Will
generate perspective and/or contour plots of the fitted
surface. 3. Spatial Process Models: Krig
3.1 Spatial Predictions
Spatial statistics refers to the class of models and methods for data
collected over a region, and informally we will refer to spatial
estimates based on a covariance model as "Kriging." Examples of such
regions might be a mineral field, a quadrat in a forest, or a
geographic region. A typical problem is to predict values of a
measurement at places where it is not observed, or, if the
measurements are observed with error, to estimate a smooth spatial
process, or surface, from the data. The Kriging function in Fields has
the advantage that it can use arbitrary covariance functions. In doing
so it is not limited to two dimensional problems or standard
models. Y_i = P(x_i) + Z(X_i) + e_i, 1
<= i <= n
where P is a low order polynomial (default
polynomial used by Krig is a linear function (m=2)). Z is a mean zero,
Gaussian stochastic process with a covariance that is known up to a
scale constant,
The returned Krig
object is the standard best linear unbiased estimate (BLUE) of f(x)
and by default the nugget variance,
The primary flexibility of the
Krig function is in specifying the covariance function and
parameters associated with it. The default covariance is the
exponential function
k(x, x') = exp( -rdist(x, x')/theta) fit <- Krig( ozone$x, ozone$y,
exp.cov, theta=100) The following examples illustrate the use of Krig and
supporting functions.
fit <- Krig(ozone$x, ozone$y,
exp.cov, theta=10)
# -- Print summary of the
Krig fit.
# -- Calculate the standard
errors of the Krig fit using the Fields function
ozone.fit.se <- predict.se( fit)
# -- It is also possible to obtain
krig predictions at other locations besides
# -- We can also use predict to obtain predictions for
the ozone fit using a
# -- Create an image plot
of the data. For fun, add the contour lines.
# -- Perform a Krig fit using exponential covariance function
with range
fit <- Krig( coalash$x, coalash$y,
cov.function = exp.cov, theta=2.5)
# -- We will use the S-Plus generic function, predict.surface
to make predictions,
fit.se <- predict.surface.se(
fit)
In the above fit, we used
the range parameter, theta=2.5. This range parameter was chosen by re-doing
the above steps with varying theta parameters and choosing the value that
yielded a small value of the GCV criterion. (The GCV minimum
is part of the Krig output object in the lambda.est. component.
Range parameters larger than 2.5 do no yield much decrease in the GCV function.
Finding an appropriate covariance function can be a
difficult modeling exercise by itself and we should note that in this
particular example identification of a covariance is
ambiguous. However, to estimate the parameters of a covariance
function, it is possible to utilize well-established
methodologies. One straightforward approach is to use nonlinear least
squares fitting of the variogram. Fields has a variogram function,
viz. vgram that helps in this
process.
coalash.vgram <- vgram( coalash$x,
coalash$y)
# -- coalash.vgram is a
list object. Where "d" are the distances,
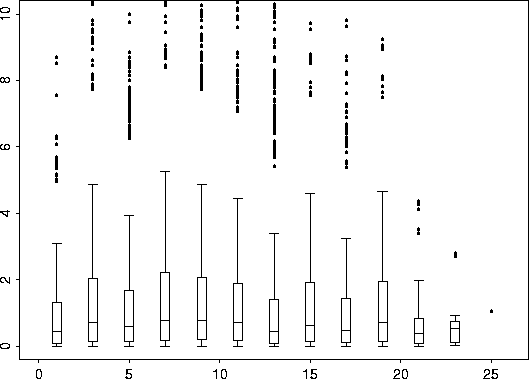
Now it is possible to plot the variogram against the distances
to get a feel for the type of covariance function, and for the parameters.
To do this, we make use of another Fields function. Namely, bplot.xy.
This function simply bins
y values according
to their x values and produces a boxplot of
these groups from binning.
bplot.xy( coalash.vgram$d, coalash.vgram$vgram)
Now we use the S-Plus function, nls
(Non Linear Least Squares Regression) to search for a suitable range parameter.
Simultaneously, we search for possible values for sigma2 and rho which
we can subsequently fix, if desired, for the Krig
fit.
vgram.fit <- nls( vgram ~ sigma2*(1-rho*exp(-d/theta)),
coalash.vgram, start=list( sigma2= 9, rho=0.95, theta=1))
summary( vgram.fit)
fit <- Krig( coalash$x, coalash$y,
theta=1.635050, sigma2=1.696190, rho=0.750553)
For daily ozone measurements it has been found that a
non-stationary covariance with an isotropic correlation function is a
useful model. Let x be a vector of locations,
Y(x) the ozone measurement at location x,
and obtain the standardized process
Z(x) = ( Y(x)
- EY(x) ) / sqrt(Var( Y(x) )) We will assume that this new process is isotropic,
and assuming that the spatial fields EY(x) and Var(
Y(x) ) are known, it is easy to use Krig to obtain
spatial estimates, incorporating this more complex covariance.
It will be handy to create a
correlogram before we continue.
ozone.cor <- COR(
ozone2$y)
The Fields function COR is useful because it will
omit missing values in computing pairwise correlations and also
contains marginal means and standard deviations. Next, we will use
this correlation object to estimate the marginal mean,
EY(x), and standard deviation, sqrt( Var(
Y(x) )) surfaces using the different days as replicates.
The use of return.matrices = F is optional and simply reduces the size
of the returned object. This way, the large matrices used in finding
the standard errors will not be included in the returned
object.
mean.tps <- Tps( ozone2$lon.lat,
ozone.cor$mean, return.matrices = F)
By plotting the computed correlations as a function
of separation distance an exponential covariance can be
identified. Similar to the previous example the parameters of the
correlation function was fit by nonlinear least squares and the range
parameter was estimated to be approximately 343 (miles).
Now we are ready to fit the
Krig model to this data, Krig does not
accept missing values, so we need to remove them in some fashion
before calling Krig. For this example, we will fit the model for day
16. exp.earth.cov is an exponential
covariance function that uses great circle distances for locations
reported in longitude and latitude. The Tps objects, sd.tps
and mean.tps are used to define the mean and
standard deviation fields for standardizing the measurements. They are
estimates of the marginal mean and standard deviation surfaces which
we use to take into account the lack of stationarity in the data
set. Since we are including a mean field, it is appropriate to fit a
constant term for the polynomial part of the model, thus we include
the option, m = 1. Finally, we use a
range parameter estimated from nonlinear least squares fitting of the
correlogram. An example of this procedure appears in the previous coal
ash example.
day16 <- c(
ozone2$y[16,])
# -- Logical vector to remove missing values from
day16.
summary( fit)
Given below is a table of covariance functions
provided by the Fields software package. It is also easy to define
your own covariance and this is described in the next section.
Defining New Covariance
Functions
The function test.cov in Fields can be used as a
template for building new covariance models. For example, it is
possible to create a new covariance function and use it with Krig to estimate a surface. The basic form is
my.fun( x1, x2), where x1 and x2 are
matrices of locations with the rows being the locations and the
columns the individual coordinates for the location. The covariance
function should return a matrix. If nrow( x1) = M, nrow( x2) = N, then my.fun( x1, x2) should return an M x N cross
covariance matrix whose (i, j) element is the covariance
between the ith row of x1 with
the jth row of x2. A handy Fields
function is rdist( x1, x2) which
computes the pairwise distance matrix between two sets of points--in
this case x1 and x2. For example, the exponential/Gaussian
covariance can be programmed as
fit <- Krig( data$x, data$y,
my.cov, range=12, p=1.5)
One caveat to creating new covariance functions is that
they must not contain an argument called "C" unless the C argument is used
in a special way.
Using the C argument
my.cov( x1, x2, C=y) For the Fields covariance functions, this matrix
multiplication is done through a FORTRAN subroutine where looping is efficient.
However this does not preclude covariance functions coded in S making
use of this feature. See exp.cov.F as an example for the details
of this extension.
Calling the Covariance Function
by Name or by Function
do.call( out$call.name, c( out$args,
list( x1, x2)))
we found that this style made it easier to port
Fields to the implementation of the S language in the R statistical
package. Note that out$call.name is
a character value that simply stores the name of the covariance function
to be called. For example, if the default exp.cov
is used, then
out$call.name is "exp.cov".
If cov.by.name is false this results in a copy of the
covariance function, with the correct arguments attached to the output
Krig
object.
The advantage is that the data, estimate and specific covariance S-function
are bundled together in a single object. Even if the covariance function
is inadvertently deleted or modified elsewhere, using the returned Krig
object will still give the correct results. The disadvantage is that the
covariance S-function is always copied and is therefore wasteful of storage.
3.5 Some Details on Tps
and Krig
Tps and Krig
The Tps estimate can be
thought of as a special case of a spatial process estimate using a
particular generalized covariance function. Because of this
correspondence the actual Tps function
is a short wrapper that determines the polynomial order for the null
space and then calls Krig with the
radial basis generalized covariance (rad.cov). In this way Tps requires little extra coding beyond the
Krig function itself and in fact the
returned list from Tps is a Krig object and so it is adapted to all the
special functions developed for this object format. One down side is
some confusion in the summary of the thin plate spline as a spatial
process type estimator. For example, the summary refers to a
covariance model and maximum likelihood estimates. This is not
something usually reported with a spline fit!
By a replicate point we mean more than one observation
made at the same location. The Fields BD data set is an example.
The Tps and Krig
functions will handle replicate points automatically, identifying replicated
values and calculating the estimate of sigma based on a pure error sums
of squares. The actual computation of the estimator is based on collapsing
the data into a set of unique locations and the dependent vector y is collapsed
into a smaller vector of weighted means. The Fields functions
cat.matrix
and fast.1way are used to efficiently identify the unique locations
and produce the replicate group means and pooled weights. Replicate points
pose several ways of performing cross-validation and this issue is discussed
below.
In writing Krig a decision was made that the Krig object can be used to find estimators for
many different values of lambda (the ratio of sigma squared to
rho). The computations to evaluate the estimator for many values of
lambda are more extensive than for just one value. In this general
case, the matrix computations are dominated by the cube of the
number of unique locations, np. The Wahba-Bates-Wendelberger algorithm
(WBW) requires an eigenvector/eigenvalue of a matrix on the order np x
np and the Demmler Reinsch algorithm (DR) requires the inverse square
root and eigenvector/eigenvalue decompositions of np size
matrices. Unlike WBW the DR is more amenable to using a reduced set of
basis functions and so it is the default for Krig. However, for consistency with other
spline implementations (e.g. GCVPACK) WBW is the default method for
Tps. The WBW decomposition is also
more stable and can produce an estimate when the DR
decomposition gives errors due to singular covariance
matrices. The user can control which is used by the decomp
argument in the call.
Reducing the number of basis
functions
The Krig estimate is a
function that is a linear combination of basis functions derived from
the covariance kernel. By default the standard Kriging estimator uses as many basis functions
as unique locations. For large problems and noisy data this may be
excessive. For example, with 1000 locations one may feel that the true
surface can be adequately approximated with far fewer degrees of
freedom than that afforded by the full set of 1000 basis functions.
To support this approximation, Krig and
Tps have the option of taking a set of
knot locations that define a basis independently of the data. The
basis functions are bump shaped functions defined by the covariance
and with the peak centered at the knot location. Thus evenly
distributing the knot locations throughout the data region may be
reasonable. One might also construct knot locations from a regular
grid, use the cover.design function to
find an irregular set of space filling points or just randomly sample
(without replacement!) the observed data locations.
Here is an example for the Midwest ozone data.
#50 points selected from the locations
that tend to be evenly distributed.
good<- !is.na(ozone2$y[12,])
# Some missing values
The warning from this fit is expected because some
estimates related to the covariance are not well defined for a reduced
basis set.
Generalized cross-validation and
choosing the smoothing parameter
The smoothing parameter, lambda is estimated by default
by minimizing the generalized cross validation function. When there
are no replicate points and a full basis is used there is no ambiguity
about the form for GCV. The basic CV strategy is to omit a part of the
data and use the model fit on the remaining data to predict the left
out observations. A good choice for some tuning parameter, such as
lambda is one that enables the model to predict subsets of the data
well when they are omitted from the fit. GCV in its standard form
finds the weighted residual sum of squares when each data point is
omitted and predicted from the remaining points. The weights depend on
the variance of the measurement error and the location of each
point. This basic form is the GCV.one criterion calculated in
gcv.Krig. However, the GCV criterion is a ratio with the numerator
being a mean, weighted residual sum of squares and the denominator
being the squared fraction of degrees of freedom associated with the
residuals. Variations on GCV used in Krig are based on modifying the
mean square of the numerator and the number of observations entering
the denominator.
For replicate points or a reduced set of basis
functions the residual sums of squares can be broken into a pure error
piece and one that is changed by the smoothing parameter. For
replicates this is the pure error sums of squares of the observations
about their group means and for a reduced basis it is the residual
sums of squares from regressing the full basis on the data. The
default GCV criterion weights these pieces separately in an attempt to
make the numerator more interpretable as an estimate of mean squared
error.
With replicate points an alternative to omitting
individual observations is to omit the entire replicate
group. Technically this is accomplished by omitting the pure error
sums of squares from the denominator of the GCV criterion. We refer to
this result as GCV.model and is less likely to over fit the data than
the other criterion.
The BD data set in Fields contains replicated points. As
an example, here are the results of different criterion applied to
this data set.
fit <- Tps(BD[,1:4], BD$lnya,
scale.type="range")
with the output
lambda trA
GCV shat
Besides these three versions of the GCV criterion
another point of flexibility is the cost parameter used in the
denominator. The default is cost=1 although specifying larger costs
will force the criterion to favor models with fewer model degrees of
freedom. For the BD example we see:
gcv.Krig( fit, cost=2)$lambda.est
with output
lambda trA
GCV shat
The warning messages are due to the fact that the global
minimum for GCV and GCV.model are at the end of the search
interval. With 15 parameters in the base polynomial model a trace of
15.01 is effectively setting lambda equal to infinity.
In the discussion given above it has been assumed that
once a GCV criterion is adopted one seeks to find the lambda value
that minimizes the criterion. We have two qualifications of this basic
approach. First in any minimization it is a good idea to examine the
criterion for multiple local minima and other strange behavior. The
plot function applied to the Krig or Tps object will plot the GCV
measures as a function of the smoothing parameter (Usually the lower
left plot in the panel of 4). It is a good idea to examine this
graph. Secondly, with replicate points, one may want the estimate of
sigma^2 implied by the curve or surface fit to agree with that
obtained from the pure error estimate. So rather than minimize a GCV
criterion one would find the value of lambda so that the two estimates
of sigma^2 are equal. In terms of the Krig object this would find
lambda so that shat.GCV and shat.pure.error are equal. The only hazard
of this estimate is when the replicates give an artificially low
representation of the error variance. One should also note that this
equality is not always possible because the pure error estimate may be
outside the range possible from the spline based estimate.
In closing we also note that one could choose lambda by
maximum likelihood. The basic function gcv.Krig could be modified to
also produce this estimate as all the necessary decompositions and
optimization functions are available.
The overall strategy for the Krig and
Tps functions is to do some extensive matrix decompositions
once and then exploit their use in finding the estimate at many
different values of lambda or even different sets of observations. In
particular the predict and gcv.Krig functions are
not limited to just the estimated values of lambda and the data vector
y used to create the Krig object. The only constraint is that if the
locations of the observations or the weighting matrix for the error
variance are changed, then decompositions must be redone. Besides
being efficient for looking at different values of the smoothing
parameter this setup also facilitates bootstrapping and
simulation.
Here are some short examples to show how this works.
Tps(ozone$x, ozone$y)-> fit
the GCV estimate gives an effective degrees of freedom
of around 4.5.
predict(fit)
evaluates the spline at this level of smoothing
predict( fit, df=8)
evaluates the spline using a model with the effective
degrees of freedom is equal to 8. This last result is equivalent to
Tps(ozone$x, ozone$y, df=8)->
fit2
but is more efficient because the decompositions are not
recreated. Instead they are reused from the fit object.
To redo the GCV search with new data one can just call
gcv.Krig with the Krig object and another y,
gcv.Krig( fit, y=ozone$y)->
gcv.out
Here is an example of a bootstrap to see the sampling
variability for GCV. Assume that the "true" function is the spline
estimate from the data. We will reuse the Krig object to get efficient
estimates when just the y's are changed.
true<- fit$fitted.values
sigma<- fit$shat.GCV
set.seed(123)
for( k in 1:50){
Within this loop we have just saved the estimated
smoothing parameter. However, an additional line calling predict with
the old object but the simulated data and new value of lambda would
give an efficient evaluation of the estimated spline.
Finally a scatterplot of the results
plot( out[,2], out[,4], xlab="eff
df", ylab="shat.GCV")
One moral from these results is to try different values
of the smoothing parameter -- although GCV usually gives unbiased
estimates, it is also highly variable.
4. Spatial Process for Large Data
Sets
The function krig.image and supporting functions
is a way to work with large two-dimensional spatial data sets. First some
back ground is given for the computations to help explain how this function
is used.
A spatial process estimate is found by solving a system
of equations for basis coefficients and multiplying the basis functions
evaluated at the points for prediction by these coefficients. Schematically
the main steps are
1) solve for x in Ax =b where A is a symmetric positive
definite matrix.
The system of linear equations is of the same size as
the the number of unique data locations and for large data sets this
system can be too large to solve explicitly. In addition the
evaluation of the estimate at a large grid of points can also be
computationally intensive.
The function krig.imagecomputes the spatial estimate
approximately using a simple iterative algorithm for solving large
linear systems. The conjugate gradient algorithm does not require the
storage of the matrix A in step 1) and is terminated by a convergence
criterion instead of providing an exact solution to the system. A key
ingredient is the necessity to multiply both A and B times an
arbitrary vector quickly. This requirement restricts the kind of
covariance functions that can be used and also explains why writing
new covariance functions for this function has more steps.
The strategy of Krig and related functions is
to be able find the estimate for many values of lambda once a set of
intensive matrix decompositions are done. For large problems this is
not feasible since the computation and storage of these matrices is
beyond the resources of S. For this reason
krig.image is limited to finding the spatial process estimate
for fixed values of lambda. Thus an analysis based on estimating the
smoothing parameter would involve calling krig.image several times with different
values for lambda.
Currently in Fields the only covariances supported are
stationary models and those based on wavelets. For stationary covariances
some extra setup has been added to make it efficient for multiplication.
This form, essentially the 2-d fast Fourier Transform of the covariance
is kept in the output argument cov.obj and can be reused for subsequent
calls to krig.image. The multiplication of
A and B work quickly because the observations and points for prediction
are located on a fine grid and to the user the most obvious difference
in the function of krig.image is the use of grids to discretize the data
and to evaluate the estimate.
Discretization of observed locations
Given a grid of points each observation location is mapped
to the closest grid point. Subsequent calculations use the grid point as
the location of the observation. If multiple points are associated with
a single grid point then the average of the dependent variables is taken
as the response and a new weight is computed for this grid
box. Even though the Discretization is necessary for the numerical algorithms,
the function is efficient enough where usually fine grids can be entertained.
In this way the spatial discretization of the problem can be set below
the level of scientific or physical interest and will not influence inferences
made from the analysis.
The data set precip
contains approximately 800 monthly precipitation
observations (for August 1963) over the central Rocky Mountain region
of the US. The locations are in longitude/latitudes. Other analysis
has suggested that the correlation range for these data is
approximately 1 degree of latitude (60 miles). We skip much of the
preliminary data analysis for this example but the reader should note
that the image functions mentioned in the last section of this
manual are useful for making spatial plots of the raw data. The
following fit discretizes the region into a 64X64 grid based on the
ranges of the data, assumes an exponential covariance function with
range equal 1.0 and a smoothing parameter equal to 0.5.
out<- krig.image( x= precip$x,
Y = precip$y,m=64,n=64,cov.function= exp.image.cov, lambda=.5, theta=1)
In this data set some locations have been omitted from
the estimation with the intent to be used for cross-validation of the model.
(Locations were chosen using cover.design.)
pred.cv<- predict( out, precip$x.cv)
In this case pred.error is an out-sample estimate for
the spatial estimate for these values of the range and lambda. To look
at the predicted surface on the basic 64X64 grid created for computing:
image.plot( out$surface)
Adding locations and a map:
points( out$x, pch=".")
Finally, the plot function will give a panel of diagnostic
plots for this fit.
plot( out)
4.3 Choosing the smoothing parameter
As part of a typical analysis one would try several different
values for lambda. If successive values of lambda are not far apart these
computations can be speeded up by using the results for one fit as the
starting values for the next. For example to fit with lambda=.25
out2<- krig.image( x= precip$x,
Y = precip$y,m=64,n=64, lambda=.25, theta=1, start= out$omega2, cov.obj=out$cov.obj)
In this example we are giving a starting vector and
also passing the efficient form for the covariance function that is
set for computation. The covariance object already has all the
information needed to compute the estimate and so the initial
specification of the covariance function is redundant. The larger
lambda is the better posed is the linear system and the convergence
will be quicker. So a search over a grid of lambda should proceed from
largest to smallest where the results from the last fit are passed as
the start values for the next lambda. In this particular example we
have found that lambda of 0.5 gives good out of sample
predictions.
4.4 Conditional simulations
and standard errors
The same reasons that make computations difficult for
the estimate also thwart the calculations of prediction standard
errors. As support for krig.image Fields has a function to sample
from the conditional distribution of the spatial model. Here we will
assume that the covariance parameters are known (fixed) and that the
field is Gaussian. The simulated fields are samples from the
conditional multivariate normal distribution for the grid locations
given the observed data. Here is an example generating 30 fields using
the first fit to the precip data given above. (This may take a
while.)
sim.krig.image( out, 30)-> look
The output object is a list with components grid and
out. The grid defines the points for evaluating the conditional
surface and the simulated surfaces are stored as a list of matrices in
the out component. For example, to plot the third simulated
field
image.plot( look$grid$x,
look$grid$y, look$out[[3]])
plot( look)
Will loop through and plot all the realizations.
sqrt( stats(look)$var )
4.5 Creating new covariance functions
The main function of a covariance function called by
krig.image is to multiply the covariance matrix found at
subset of the grid points with an arbitrary vector. Recall that
everything in krig.image happens with respect to locations on the
specified grid. Let loc1
and loc2 be two matrices of
subscripts for grid locations. Each matrix has two columns and the row
indicates the two subscripts for an element in the grid. The
covariance function call follows the template
cov.function(loc1,loc2, temp)->
out
Here temp is a vector
of length
nrow( loc2) and the result
is S%*%temp where Siso
the cross covariance matrix between the locations indexed by loc1
and
loc2.
S
has
dimensions
nrow(loc1)
by nrow(
loc2). If one of the index arguments is missing it is assumed that
all grid points are included for the multiplication. The reader is referred
to the code for exp.image.cov to
see a particular implementation of this format. The other feature of the
covariance is to setup the calculations to make subsequent calls efficient.
In the case of the stationary covariance function this involves finding
the FFT once for the covariance and returning this result. Setup features
are implemented by setting the argument setup equal to true. Subsequent
calls should pass this returned object from this call as the argument cov.obj.
This setup is also needed to simulate stationary random fields with the
sim.rf function. For example
grid<- list( x= 1:64, y=1:64)
Now do the (fast) multiply:
exp.image.cov(loc1, loc2, temp,
cov.obj=cov.obj)-> result
or simulate a field
sim.rf( cov.obj)-> result2
The wavelet covariance function typically does not require
a setup step.
5. Simulating Random Fields sim.rf
Given the covariance function for a Gaussian random field
one would like to simulate a realization of this surface.
To make a point about computation we first outline the
conventional way in S code and using some Fields functions. Suppose one
wanted to simulate a 2-d process with exponential covariance, range parameter
theta equal to 1.5 on a grid. First create a grid of 15X15 points.
xg<- make.surface.grid( list(
seq(0,5,,15), seq( 0,5,,15)))
Find the covariance matrix among these points
Note that Sigma is a 225X 225 matrix.
Sigma.half<- chol( Sigma)
OK now simulate the field
f<- Sigma.half%*% rnorm( 225)
Reformat as an image and take a look
as.surface( xg, f)-> out
The only problem with this approach is the
computations and storage grow rapidly for larger grids. For example a
128X128 image would mean that the dimension of Sigma would be huge, 16K X 16K, and
effectively prohibit the use of the Cholesky decomposition within
S. For rectangular grids one can sometimes simulate Gaussian random
fields very efficiently using an alternative algorithm based around
the Fast Fourier Transform. For background see Chen and ???
(19??). The restrictions are that the covariance function needs to be
stationary and the correlation needs to the small relative to the
domain. The Fields function sim.rf
implements this approach for the 2-d case. Here is an example
simulating the same exponential covariance process but on a finer
grid. Define the x and y spacing for the grid
grid<- list( x=seq( 0,10,,128),
y=seq( 0,10,,128))
Setup by finding the FFT of the covariance.
exp.image.cov( grid=grid, theta=1.5,
setup=T)-> cov.obj
In this example one can now repeatedly call sim.rf
using the same covariance object to get different random fields. The set
up step just needs to be done once.
There is an important limitation to this method of
simulation. If the correlation range is too large relative to the
grid limits, the FFT of the covariance will not be positive. In this
case sim.rf will return an error and not try to use the
object. The practical fix is to make the grid larger until the FFT of
the covariance is positive definite.
Back to top
6.1 Space-Filling Designs: cover.design As a companion to the curve and surface fitting in Fields
we have found it useful to have an algorithm that will produce sets of
points that are evenly distributed. A typical application is to choose
a subset of observed locations to use as the knots for a reduced set of
basis function (see the example above). This subset should be evenly
distributed over the observed domain of data. The function
cover.design is
a function to accomplish this. The basic framework is to determine a subset
of design points from a larger set of candidate points. The candidate points
not only serve as possible design points but determine the coverage criterion.
A design's quality is evaluated by how well it covers the candidate set
and a design is improved by swapping a point from the candidate set with
a design point that produces a smaller coverage criterion.
Coverage Criterion
At this point an analogy may be helpful to explain the
coverage criterion. Suppose that you are charged with locating a fixed
number of convenience stores in a city. Given a particular set of store
locations each resident will have a store that is closest to their home.
Out of all the residents, find the one who is farthest to their nearest
store. This is the maximum over the nearest neighbor distances. A good
design for the stores makes this criterion as small as possible. In words,
one seeks to minimize the distance the residents must travel to their closest
convenience store. The result is referred to as the minimax design.
Swapping Algorithm
The cover.design
function has two approximations. The minimax criterion is
approximated by a smoother criterion based on L_p norms. These are the
P and Q arguments in the call. The defaults P=Q=32 appear to yield a
good approximation to the minimax designs. The other approximation is
that the coverage criterion is minimized by updating one design point
at a time. For each design point one checks whether a swap with a
candidate point will yield a smaller coverage criterion. If such a
swap is found the swap is made: the new point is adopted as part of
the design and the old design point is moved into the candidate set.
This process continues until no more productive swaps can be made or
the number of iterations is exceeded. This algorithm is not guaranteed
to give a global minimum and so one may not obtain the optimal design
solution. However, we have found this algorithm to give useful
designs even if they are not the global minimizer. In general, the
global minimum is difficult to find and has questionable added value
over good approximate solutions.
Fixed design points and other distance functions
There are several important features of the cover.design function related to the
algorithm for An example nesting one design in another.
Here is a simple example to thin out a random set of 2-d
locations and shows how the fixed point option works.
Create 200 locations uniformly distributed in the unit
square.
set.seed( 123)
Now find a coverage design of 10 points
cover.design(cand, 10)-> design10
The component design10$design is
the best design and design10$best.id gives
the row numbers of the candidate set matrix that comprise the best design.
Check it out
plot( design10)
Call:
Number of design points:
10
History:
The table shows the swapping history . For example
on the second step the 34th candidate point is replaced by number
15.
Now add 20 more points for a total of 30
design30<- cover.design(
cand, 30, fixed=design10$best.id)
Here is what happened:
plot( cand, pch="o")
Note that the 10 point design has kept two points
unusually close. This problem could be fixed by requiring more random
starts. Setting nruns=5 gives a design with a lower cover
criterion.
In the course of spatial analysis of 2-d fields we found
need for some simple functions to create, plot, and smooth rectangular
images. Here we mention two, as.image and image.plot. By a surface or image
object we mean a list with components x, y and z Where x and y are equally
spaced grids and z is a matrix of values. This is the same format as used
by the S functions contour, image, and persp
as.image
The required argument for
as.image is Z, the values
for the image and the most common optional argument is x; a 2 column matrix
with the spatial locations of Z.
as.image( precip$y, x=
precip$x)-> out.p
the default is a 64X64 grid using the ranges of
the data. One can specify alternative grids for example
grid<- list( x=seq( -111,
-98,,25), y=seq( 35, 45,,40))
gives a 25X40 point discretization.
Several other useful options are being able to
specify weights to use in finding a weighted mean for each box
or to just give the number of grid points and use the ranges of
the data for gridding. The output list in addition to x,y, and z
components has the counts (N), the indices of
the nonmissing boxes (ind) and sum of the weights for each
nonmissing box (weights).
image.smooth and smooth.2d
Here is an example smoothing the precip data set and
plotting the smoothed image.
out<- smooth.2d( precip$y,
x=precip$x, theta=1.0)
image.plot( out)
image.plot
look <- as.image( coalash$y,
x = coalash$x)
The function image.plot has the same functionality as
image but adds a legend strip. It can be used to add a legend strip to
an existing plot or create a new image and legend. Its chief benefit
is that this function resizes the plot region automatically to make
room for the legend strip. We have found a function with reasonable
defaults has been quite useful. The argument horizontal if
true will put the legend strip under the plot. ( default is false).
One effective graphical plot is a panel of images on a similar scale
and plot region size but with only one legend
strip. image.plotmakes
this fairly easy to do. For example to show the coalash data at
several discrtetizations
set.panel( 3,1)
# or par( mfcol=c(3,1)))
image( as.image( coalash$y,
x = coalash$x,
image(as.image( coalash$y,
x = coalash$x,
as.surface and make.surface.grid
These two functions were created to make it easy to
create grids of points and to convert a vector evaluated on this grid
into a surface object. make.surface.grid takes a list with
information about the grid ranges and the number of points in each
dimension and returns a matrix with all the grid locations.
grid<- list( x=seq( -111,
-98,,25), y=seq( 35, 45,,40))
The result of the last step is a (25x40) by 2
matrix where the rows are the locations of all grid points.
grid.locs also has some attributes attached that contain
information from the list used to define the grid.
Often after evaluating a function on a grid one would
like to reform the results as a surface. As a specific example suppose
fit is the output object from Krig
predict( fit, grid.locs)-> look
The result will be a list with x,y,and z components suitable
for plotting with functions such as persp, image or contour.
1. the total number of observations including replicates.
plot(ozone.tps)
2. the total number of unique points.
3. the maximum degree of polynomial (m - 1) included in the
spline model.
4. total number of polynomial terms up to the maximum
degree. This is the total number of conventional parameters for the
spline.
5. total number of effective parameters associated with the
spline curve including those of the polynomial. This number is
controlled by the parameter 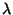 and is the trace of
the smoothing matrix, A(
and is the trace of
the smoothing matrix, A(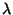 ).
).
6. spline degrees of freedom subtracted from the total number
of observations.
7. estimate of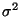 by maximum
likelihood.
by maximum
likelihood.
8. estimate of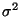 by using residual sum of
squares and effective d.f.
by using residual sum of
squares and effective d.f.
9. - 11. these are explained in the discussion of the Krig
function and the spatial model.
12. value of smoothing parameter used to find spline
estimate. If no value has been specified, the smoothing parameter
estimated by GCV is reported.
13. value of cost parameter.
14. value of GCV function at 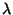 . This is
an estimate of the average squared prediction error for a given value
of
. This is
an estimate of the average squared prediction error for a given value
of 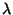 . If
. If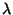 has been
estimated, then the minimum value of the GCV function is reported.
has been
estimated, then the minimum value of the GCV function is reported.
[1] 38.35702 38.62821 38.44499
39.01395 38.79481 39.72864 38.30791 39.35719 [9] 39.19664
39.63307 40.98843 40.05890 41.11455 40.87318 41.42214 40.35936 [17]
40.03565 39.10773 41.34989 40.83722
The estimate can be evaluated at other locations by including
a matrix with these locations in predict.
Fields assumes a spatial model of the form
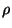 k(x, x') and
denote the variance of e_i by
k(x, x') and
denote the variance of e_i by 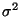 /W_i.
Consistent with the spline estimate, we take
/W_i.
Consistent with the spline estimate, we take 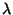 =
= 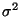 /
/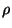 . The covariance function, k, may also depend on other
parameters that we explain how to specify below but these are not
estimated directly by the Krig function. Throughout this discussion
the reader should keep in mind that a low order polynomial, fixed
effect is also part of the estimate. By default this is a linear
function in the spatial coordinates but the degree can be
changed.
. The covariance function, k, may also depend on other
parameters that we explain how to specify below but these are not
estimated directly by the Krig function. Throughout this discussion
the reader should keep in mind that a low order polynomial, fixed
effect is also part of the estimate. By default this is a linear
function in the spatial coordinates but the degree can be
changed.
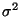 , is found by
GCV. If one assumes a Gaussian process and Gaussian errors, then this
estimate is also related to the conditional expectation of f(x) given
the observed data. Of equal value are estimates of the standard errors
of prediction and more will be said about these below.
, is found by
GCV. If one assumes a Gaussian process and Gaussian errors, then this
estimate is also related to the conditional expectation of f(x) given
the observed data. Of equal value are estimates of the standard errors
of prediction and more will be said about these below.
If ![]() or df are not passed into Krig, then Krig estimates
or df are not passed into Krig, then Krig estimates ![]() (lambda) by
(lambda) by ![]() .
If
.
If ![]() and
and 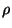 are
not passed, then Krig will use Generalized Cross Validation (GCV) to
estimate them. This is the case in the example above.
are
not passed, then Krig will use Generalized Cross Validation (GCV) to
estimate them. This is the case in the example above.
Back to top
Ozone Concentrations in Chicago
(Data obtained from Gomez and Hazen (1970, Tables 19
and 20) on coal ash for the Robena Mine Property in Greene County
Pennsylvania.)
Daily 8-hour surface ozone measurements during the summer
of 1987 for approximately 150 locations in the Midwest.
# -- Exponential covariance function. Choice of range
parameter, theta, is
# -- arbitrarily chosen here to be 10 miles.
# -- The summary function
is a generic S-Plus function that is used to provide
# -- summary information about a regression object. For
example, from the
# -- output of the summary below, we can discern that
4 or 5 parameters
# -- (Effective df=4.5) are needed to fit the model.
Also, the estimate for
# -- sigma is about 4.2 (both MLE and GCV give this),
and for rho is 2.374.
summary( fit)
Call:
Krig(x = ozone$x, Y = ozone$y, cov.function = exp.cov, theta = 10)
Number of Observations: 20
Number of unique points: 20
Degree of polynomial null space ( base model): 1
Number of parameters in the null space 3
Effective degrees of freedom: 4.5
Residual degrees of freedom: 15.5
MLE sigma 4.206
GCV est. sigma 4.2
MLE rho 2.374
Scale used for covariance (rho) 2.374
Scale used for nugget (sigma^2) 17.69
lambda (sigma2/rho) 7.453
Cost in GCV 1
GCV Minimum 22.8
Residuals:
min 1st Q median 3rd Q max
-7.037 -2.189 -0.4681 2.299 7.382
REMARKS
Covariance function: exp.cov
# -- Obtain diagnostic plots
of the fit using the generic function, plot.
# -- This is the same function used for other standard
S-Plus regression
# -- objects. Note that the plots of the residuals suggest
that the model is
# -- overfitting ozone at lower values.
plot( fit)
# -- predict.se.Krig, which
finds the standard errors of prediction based on a linear
# -- combination of the observed data--generally the
BLUE. The only required
# -- argument is the Krig object itself. Optional arguments
include alternate
# -- points to compute the standard error on, viz. x,
a covariance function, rho, sigma2
# -- (default is to use the values passed into Krig
originally),
# -- and some other logical parameters that can be found
in the help file.
out.p <- predict.surface( fit)
image.plot( out.p, xlab="East-West",
ylab="North-South")
out2.p <- predict.surface.se(
fit)
contour( out2.p, add=T)
# -- those given with the data. For example,
# -- Here, we choose a random set of points to
predict at. I did this to
# -- emphasize that you can choose any grid points that
you want
# -- to study.
loc.knot <- cbind (runif( 20,
min=-30, max=35), runif( 20, min-21, max=36))
# -- Now predict with these points.
ozone.pred2 <- predict( fit,
loc.knots)
# -- different value for lambda, or df--and, indeed,
different data.
# -- For example,
ozone.pred3 <- predict( fit,
lambda=5)
Data obtained from Gomez
and Hazen (1970, Tables 19 and 20) on coal ash for the Robena Mine
Property in Greene County Pennsylvania.
look <- as.image( coalash$y,
x=coalash$x)
image.plot( look)
contour( look, add=T, labex=0)
# -- parameter, theta=2.5 (choice of theta will be explained
below).
summary( fit)
Call:
Krig(x = coalash$x, Y = coalash$y, cov.function = exp.cov.S)
Number of Observations: 208
Number of unique points: 208
Degree of polynomial null space ( base model): 1
Number of parameters in the null space 3
Effective degrees of freedom: 29.7
Residual degrees of freedom: 178.3
MLE sigma 1.02
GCV est. sigma 1.018
MLE rho 0.2829
Scale used for covariance (rho) 0.2829
Scale used for nugget (sigma^2) 1.04
lambda (sigma2/rho) 3.675
RESIDUAL SUMMARY:
min 1st Q median 3rd Q max
-2.169 -0.6578 -0.09917 0.4115 6.169
COVARIANCE MODEL: exp.cov.S
DETAILS ON SMOOTHING PARAMETER:
Method used: GCV Cost: 1
lambda trA GCV GCV.one GCV.model shat
3.675 29.69 1.209 1.209 NA 1.018
Summary of estimates for lambda
lambda trA GCV shat
GCV 3.675 29.69 1.209 1.018
GCV.one 3.675 29.69 1.209 1.018
plot( fit)
# -- using the Krig object
fit.
One could generate a grid of points and use just the predict function
# -- but for most cases the defaults in predict.surface
give a quick and useful result.
# -- We also added the contours of the standard errors
of the estimates.
fit.pred <- predict.surface(
fit)
image.plot( fit.pred)
contour( fit.se, add=T)
# -- coalash.vgram$vgram
is the variogram, and call tells how the vgram
function was called.
names( coalash.vgram)
[1] "d"
"vgram" "call"
Indeed, the plots might suggest an alternative covariance
matrix to the exponential. Never-the-less, for the purpose of demonstrating
the software, we will use the exponential covariance function.

Formula: vgram ~ sigma2 * (1 - rho * exp( - d/theta))
Parameters:
Value Std. Error t value
sigma2 1.696190 0.0334569 50.69770
rho 0.750553 0.2807990 2.67292
theta 1.635050 0.5580010 2.93019
Residual standard error: 3.60828 on 21523 degrees of freedom
Correlation of Parameter Estimates:
sigma2 rho
rho -0.346
theta 0.566 -0.877
These results suggest theta = 1.63505, and we can also try
fixing sigma2 = 1.696190 and rho = 0.750553.
summary( fit)
CALL:
Krig(x = coalash$x, Y = coalash$y, rho = 0.750553, sigma2 = 1.69619, theta =
1.63505)
Number of Observations: 208
Number of unique points: 208
Degree of polynomial null space ( base model): 1
Number of parameters in the null space 3
Effective degrees of freedom: 48.8
Residual degrees of freedom: 159.2
MLE sigma 0.9604
GCV est. sigma 0.9647
MLE rho 0.4082
Scale used for covariance (rho) 0.7506
Scale used for nugget (sigma^2) 1.696
lambda (sigma2/rho) 2.26
RESIDUAL SUMMARY:
min 1st Q median 3rd Q max
-1.899 -0.5541 -0.1009 0.3808 5.486
COVARIANCE MODEL: exp.cov
DETAILS ON SMOOTHING PARAMETER:
Method used: user Cost: 1
lambda trA GCV GCV.one GCV.model shat
2.26 48.8 1.216 1.216 NA 0.9647
Summary of estimates for lambda
lambda trA GCV shat
GCV 3.422 37.27 1.213 0.9979
GCV.one 3.422 37.27 1.213 0.9979
From this we see that the MLE sigma has been reduced to 0.9064
from 1.02. The GCV minimum is a little higher, and the effective degrees
of freedom has been increased to 48.8 from 29.7 when we used GCV to find
sigma2, rho, and subsequently lambda.
The Fields data set ozone2 consists of daily 8-hour surface
ozone measurements during the summer of 1987 for approx. 150 locations
in the Midwest.
plot( ozone2$lon.lat, pch="o")
# US is a handy Fields function
using the maps library from Splus
US(add=T)
title("Daily 8-Hour Ozone Data,"
cex=0.85)
sd.tps <- Tps( ozone2$lon.lat,
ozone.cor$sd, return.matrices = F)
The details of this analysis are part of the Fields
demo along with more extensive analysis of this data.
idn <- !is.na( day16)
fit <- Krig(
ozone2$lon.lat[idn, ], day16[idn], cov.function=exp.earth.cov, theta =
343, sd.obj=sd.tps, mean.obj=mean.tps, m=1)
Krig(x = ozone2$lon.lat[idn, ], Y = day16[idn], cov.function = exp.earth.cov,
m = 1, mean.obj = mean.tps, sd.obj = sd.tps, theta = 343)
Number of Observations: 147
Number of unique points: 147
Degree of polynomial null space ( base model): 0
Number of parameters in the null space 1
Effective degrees of freedom: 114.7
Residual degrees of freedom: 32.3
MLE sigma 0.289
GCV est. sigma 0.3172
MLE rho 7.538
Scale used for covariance (rho) 7.538
Scale used for nugget (sigma^2) 0.0835
lambda (sigma2/rho) 0.01108
Cost in GCV 1
GCV Minimum 0.4585
Y is standardized before spatial estimate is found
Residuals:
min 1st Q median 3rd Q max
-0.6091 -0.07774 0.003612 0.08233 0.433
REMARKS
Covariance function: exp.earth.cov
From the above summary, we can see that there are
147 observations, all of which are unique. A constant term was used
for the polynomial part of the model--as we specified with m = 1. The large effective degrees of freedom
in the model (114.7) found by GCV will result in a surface that fits
the observations closely. Note that the GCV function (left lower
graph) is fairly flat from 30 d.f. and suggests that the value of
lambda can not be well estimated from in sample average prediction
error.
Solving large linear
systems
Table - Covariance functions in Fields
Name/
description S-Function
optional arguments
with defaults Fortran/S
version C argument
Exponential/
Gaussian exp.cov
theta = 1, p = 1
both
yes
Exponential
for sphere exp.earth.cov
theta = 1
S
no
Matern
matern.cov
smoothness = 0.5
range = 1FORTRAN
no
Periodic 1-d
periodic.cov.ld
a = 0, b = 1
both
no
Cylindrical
periodic.cov.cyl
a = 0, b = 365
theta = 1 S
no
Poisson covariance
for the sphere poisson.cov
eta = 0.2
S
no
Sample covariance
test.cov
theta = 1
S
no
Generalized spline
covariance rad.cov
p
both
yes
my.cov <- function( x1, x2, p = 1, range=1) {
cov <- exp( - (rdist(x1, x2)/range)^p)
return( cov)
}
Then, to use this function with Krig, simply include its name along with any
parameters to be passed in. That is,
Some of Fields covariance functions have an additional
argument and function that can be exploited
in the spatial process fucntions. Suppose that
Sigma = my.cov( x1, x2)
is the covariance matrix, and y is a vector of length = nrow(
x2) one requires the result
will return the usual cross covariance matrix.
(cov.by.name logical parameter)
What in the world does this parameter do? The Krig function
and supporting functions can keep track of the covariance function in two
ways. One way, "by value" is making a local copy of the covariance
function and changing the default calling arguments to those specified
when Krig was called. The second way "by name" just the
name of the covariance function is kept and an argument list is created
of the arguments for the covariance when Krig was called. cov.by.name
is a logical parameter (default = T) that controls which way
this is done for the Krig output object.
When cov.by.name is true, the Fields
functions it will use the standard S function do.call to
evaluate the covariance function. The optional arguments specific
to the particular covariance function are stored in a list object called
"args" that holds all other pertinent information. This is convenient for
passing parameters from one function to another. For example, instead of
finding the covariance matrix, k(x1, x2), by using the function directly--i.e.
cov.function(
x1, x2, ...)--the function evaluation for example within
Krig would proceed by:
knots <- cover.design(
ozone2$lon.lat, 50)$design
x<- ozone2$lon.lat[good,]
y<- c( ozone2$y[12,good])
Tps( x, y, knots=knots)-> out
[1] "Maximum likelihood estimates
not found with knots \n \n "
fit$lambda.est
GCV
0.0017638586 26.78111 6.486331 1.2851278
GCV.model 0.0006164361
35.71981 7.316078 1.0459907
GCV.one 0.0001229511
47.97921 21.698684 0.8305018
RMSE
NA NA
NA NA
pure error 0.0001109830 48.52083
24.530808 0.8252884
GCV
2.1553372865 15.01580 7.586782 1.7601200
GCV.model 2.1553372865
15.01580 7.586782 1.7601200
GCV.one 0.0035109339
22.25720 10.974231 1.4402488
RMSE
NA NA
NA NA
pure error 0.0001109830 48.52083
NA 0.8252884
Warning messages:
1: GCV search gives a minimum
at the endpoints of the grid search in: Krig.find.gcvmin(info, lambda.grid,
gcv.grid$GCV, Krig.fgcv,
2: GCV search gives a minimum
at the endpoints of the grid search in: Krig.find.gcvmin(info, lambda.grid,
temp, Krig.fgcv.model, tol = tol,
predict( fit2)
out<- matrix(NA, nrow=50,
ncol=4)
y<- true + rnorm(20)*sigma
gcv.Krig( fit, y=y)-> temp
out[k,] <- temp$lambda.est[1,]
}
and
2) evaluate Bx where B are the solution basis functions
evaluated at the locations for prediction.
pred.error<- sqrt(mean(
(pred.cv- precip$y.cv)^2))
US( add=T)
The simulations will have a population mean equal to
the spatial estimate and the variance about the this mean is the prediction
variance using the spatial model. This is also the posterior variance from
a Bayes perspective. One way to approximate this variance is to find the
sample variance at the grid points.
stats( look)
computes means and variances at the grid points and so
a model based standard error of prediction at the grid points is:
exp.image.cov(grid= grid,
setup=T, theta=4)-> cov.obj
Sigma<- exp.cov(xg,xg,
theta=1.5)
Cholesky square root of this matrix.
image.plot( out)
sim.rf(cov.obj)-> out
image.plot( out)
finding the design. One can fix some points in the
design. These are simply points that are not allowed to be swapped
out. This is useful if one wants to build up a sequence of designs of
increasing size with the smaller designs being subsets of the larger
ones. Although the default is to use Euclidean metric to measure
distance between points, any S function that is a metric can be
substituted for this choice. See the help file for an example using
Manhattan distance. Finally the swapping algorithm may only
consider swapping candidate points that are near neighbors of the
design point. This is helpful when the candidate set is large.
cand <- matrix( runif( 200*2),
ncol=2)
summary( design10)
cover.design(R = cand, nd =
10)
Number of fixed points:
0
Optimality Criterion:
0.3524
step swap.out swap.in
new.crit
0
0 0 0.5071
1
34 15 0.4816
2
73 35 0.4224
3
58 120 0.3524
points( design10$design, pch="X",
cex=2.0)
points( design30$design, pch="+",
cex=2.0
This function creates an image object from irregular
x,y,z by discretizing the 2-d locations to a grid and then producing an
image object with the z values in the right cells.
The basic idea is that each observation is identified
with a grid box and the mean value for all observations
is returned for that box. If no observations fall into a particular
box an NA is returned for that location. Missing values are convenient
because they are handled nicely by the contouring and image functions.
To grid the
precip data and plot it
image( out.p)
as.image( precip$y, precip$x,
grid=grid)-> out.p
Two functions in Fields that will smooth 2-d
data using a kernel estimate. image.smooth requires the data in the
form of an image matrix but can handle missing values for cells.
smooth.2d takes as input irregular data but then discretizes it to
a regular grid, possibly with missing cells and applies the same smoothing
operations as image.smooth. In both cases the default kernel function
is an exponential, although different kernel forms can be specified.
For the exponential the bandwidth parameter is passed as the argument
theta.
This function simply draws an image plot
with a color legend along side.
image.plot (look)
par( pty="s") #
square plotting regions
image.plot( as.image( coalash$y,
x = coalash$x))
ncol=32,nrow =32))
ncol=16, nrow=16))
grid.locs<-make.surface.grid(
grid)
as.surface( grid.locs, look)->
look.surface
Back to top